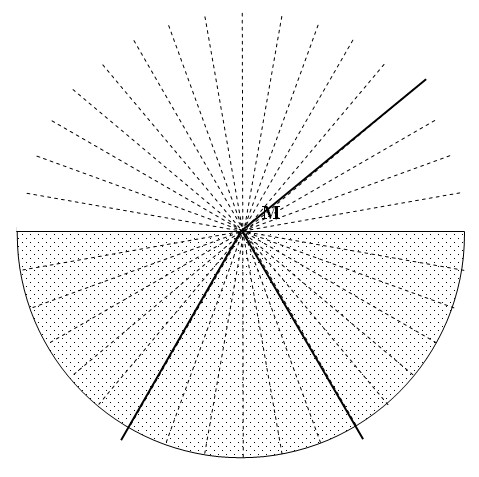
In de tekening is het verloop van een invallende lichtstraal getekend.
Hoe groot is de hoek van inval en hoe groot is de hoek van breking?
1. 30° en 50°
2. 60° en 40°
3. 50° en 30°
4. 40° en 60°
5. Dat weet je niet omdat niet te zien is waar de straal vandaan komt.
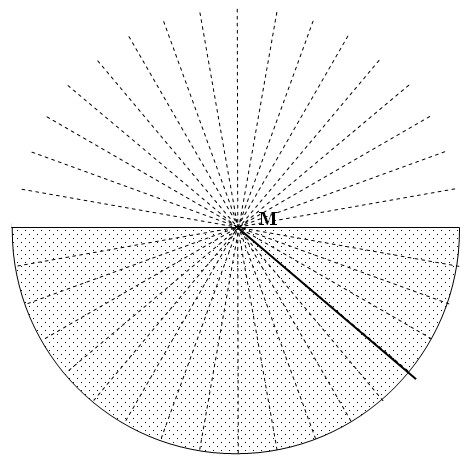
In de tekening zie je een invallende lichtstraal.
De grenshoek van het materiaal is 40°.
Zal er breking optreden? Zo ja naar de normaal toe of er van af?
1. Nee
2. Ja, naar de normaal toe.
3. Ja, van de normaal af.
4. Nee want er is geen gebroken straal getekend.
5. Dat kun je niet weten omdat de gereflecteerde straal en de gebroken straal niet getekend zijn.
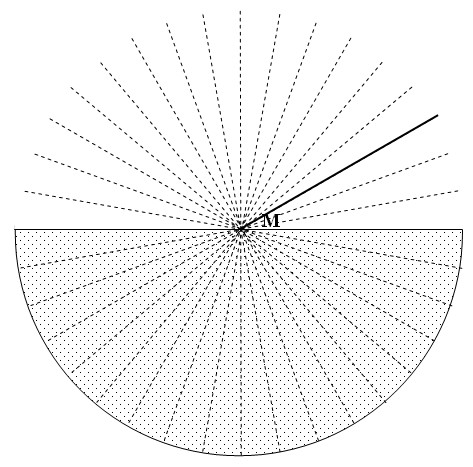
In de tekening zie je een invallende lichtstraal.
De grenshoek van het materiaal is 40°.
Zal er breking optreden? Zo ja naar de normaal toe of er van af?
1. Ja, naar de normaal toe.
2. Ja, van de normaal af.
3. Nee want i > g
4. Ja want i > g
5. Dat kun je niet weten omdat de gereflecteerde straal en de gebroken straal niet getekend zijn.
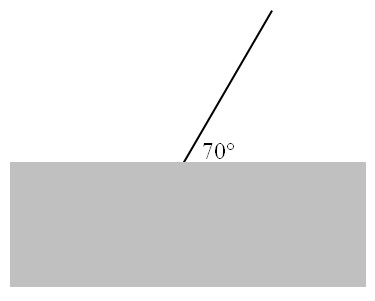
In de tekening zie je een invallende lichtstraal.
Van de stof is de brekingsindex 2,0.
Je wilt de hoek van breking berekenen.
In BINAS vind je de formules ∟i = ∟t, sini/sinr = n en sing = 1/n
Welke waarde moet je invullen voor i en welke waarde voor n?
1. i = 20° en n = 2,0
2. i = 70° en n = 2,0
3. i = 20° en n = 0,50
4. i = 20° en n = 0,20
5. i = 70° en n = 0,50
6. i = 70° en n = 0,50
7. i = 70° en n = 0,20
In de tekening zie je een invallende lichtstraal.
De grenshoek van het materiaal is 60°.
Zal er breking optreden? Zo ja naar de normaal toe of er van af?
1. Ja, van de normaal af.
2. Nee want i < g.
3. Nee want i > g
4. Nee want er is geen gebroken straal getekend.
5. Dat kun je niet weten omdat de gereflecteerde straal en de gebroken straal niet getekend zijn.
6. Ja, naar de normaal toe.
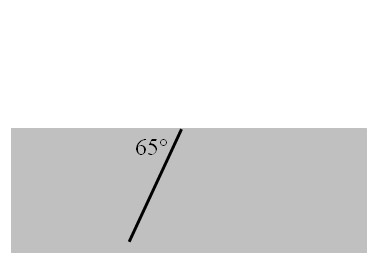
In de tekening zie je een invallende lichtstraal.
Van de stof is de brekingsindex 2,0.
Je wilt de hoek van breking berekenen.
In BINAS vind je de formules ∟i = ∟t, sini/sinr = n en sing = 1/n
Welke waarde moet je invullen voor i en welke waarde voor n?
1. i = 25° en n = 0,50
2. i = 65° en n = 2,0
3. i = 25° en n = 2,0
4. i = 25° en n = 0,20
5. i = 65° en n = 0,50
6. i = 65° en n = 0,20
Van een stof is de brekingsindex 1,6.
In BINAS vind je de formules ∟i = ∟t, sini/sinr = n en sing = 1/n
Hoe groot is de grenshoek? Gebruik je rekenmachine.
1. 39°
2. 0,68°
3. 0,625°
4. 1,6°
5. 49°
Waarom breekt een lichtstraal als hij van lucht naar een stof gaat?
1. Omdat licht in de stof langzamer gaat dan in lucht.
2. Omdat de dichtheid van de stof groter is dan van lucht.
3. Omdat de hoek van breking kleiner is dan de hoek van inval.
4. Omdat de hoek van breking groter is dan de hoek van inval.
5. Omdat licht in de stof sneller gaat dan in lucht.
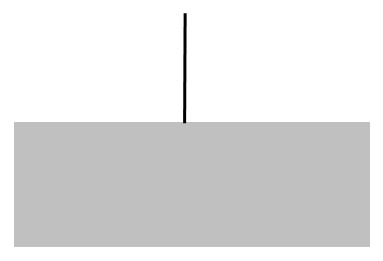
In de tekening is de invallende lichtstraal getekend.
Hoe groot is de hoek van inval?
1. 0°
2. 90°
3. Er is geen hoek van inval.
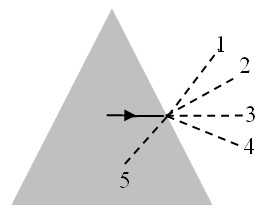
In de tekening zie je een lichtstraal die het glas uit wil.
Welke stippellijn geeft de gebroken straal juist weer?
1. 4
2. 1
3. 2
4. 3
5. 5
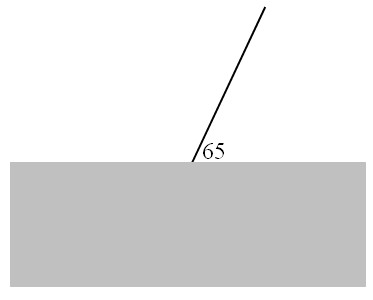
In de tekening zie je een invallende lichtstraal.
De brekingsindex van de stof is 1,5.
In BINAS vind je de formules ∟i = ∟t, sini/sinr = n en sing = 1/n
Hoe groot is de hoek van breking? Gebruik je rekenmachine.
1. 16°
2. 17°
3. 43°
4. 39°
5. Er is geen breking.
In de tekening zie je een invallende lichtstraal.
De brekingsindex van de stof is 1,5.
In BINAS vind je de formules ∟i = ∟t, sini/sinr = n en sing = 1/n
Hoe groot is de hoek van breking? Gebruik je rekenmachine.
1. 39°
2. 33°
3. 13°
4. 37°
5. Er is geen breking.
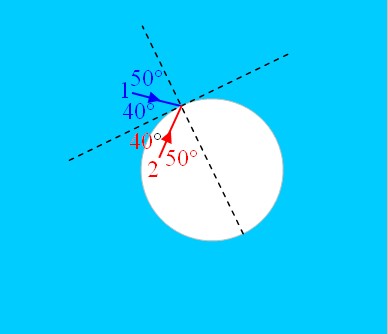
In de tekening zie je een luchtbel onder water. Je ziet ook straal 1 (blauw) en straal 2 (rood).
De grenshoek van water is 49°.
Wat gebeurt er met straal 1 en wat gebeurt er met straal 2?
1. Straal 1 wordt totaal gereflecteerd. Straal 2 breekt naar de normaal toe.
2. Straal 1 wordt totaal gereflecteerd. Straal 2 wordt totaal gereflecteerd.
3. Straal 1 breekt van de normaal af. Straal 2 breekt naar de normaal toe.
4. Straal 1 breekt van de normaal af. Straal 2 wordt totaal gereflecteerd.

Lichtbreking bovenbouw